Leonhard Euler es uno de los mayores maestros de la humanidad. Es prácticamente imposible encontrar una sola disciplina del saber científico en la que este gigante de las matemáticas y de la inteligencia no haya realizado una aportación esencial. Su majestuosa contribución al conocimiento se desarrolla a lo largo del siglo XVIII y para encontrar obras de semejante calibre es preciso esperar hasta el s XIX en el que desarrollan sus carreras matemáticos de la talla de Gauss, Riemann o Cauchy.
Entre las numerosísimas anécdotas que muestran la portentosa capacidad intelectual de este matemático suizo puede citarse que se sabía de memoria la Eneida en latín, asi como las actas completas de la Academia Prusiana de Ciencias o las primeras seis potencias de los primeros cien números primos.
Vamos a hablar de la llamada 'recta de Euler', un resultado de geometría de triángulos que requiere la presentación de algunos conceptos interesantes. Empezaremos considerando el baricentro, o centro de masas del triángulo. Es el punto de intersección de las tres medianas. La mediana es la recta que une el lado medio de un lado con el vértice opuesto. Para aclarar el gráfico únicamente representamos dos de ellas:
Consideremos ahora el lugar donde se cruzan las alturas del triángulo. Las alturas son las perpendiculares a los lados que pasan por el vértice opuesto. El punto de corte de las alturas se denomina ortocentro. De nuevo representamos únicamente dos de estas alturas:
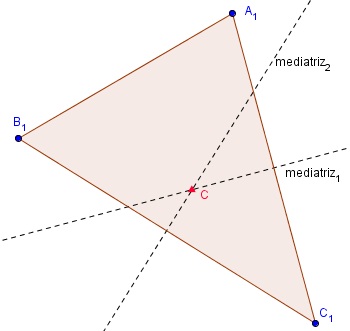
Y vamos a considerar un tercer punto notable del triángulo: el circuncentro, que es el lugar donde se cruzan las mediatrices. Las mediatrices son las rectas perpendiculares a los lados que pasan por el punto medio de estos. Veamos de nuevo el gráfico:
El circuncentro es un lugar muy importante, ya que es el centro de la circunferencia que pasa por los tres vértices del triángulo, como indica su nombre. Veámoslo:
Euler demostró que los tres puntos presentados (baricentro, ortocentro y circuncentro) se disponen según una recta a la que denominamos 'recta de Euler' en su honor. Veamos un par de ejemplos:
En este segundo ejemplo vamos a representar un triángulo con un ángulo obtuso. Como veréis, esto hace que el circuncentro y el ortocentro caigan fuera de la superficie del triángulo considerado, mientras que el baricentro se mantiene siempre en el interior.